I have never reflected so far on the concept of the meridian, and even less on the meridians we can draw anywhere on the basis of a light spot at noon.
However, I have known this spot – and quite far from Bologna.
It runs, month after month, on the great meridian of the former hospital in Tonnerre, founded in 1293 by Margaret of Burgundy, widow of Charles of Anjou, King of Sicily.


The meridian – called here, probably incorrectly, a gnomon – is 17 meters long. It was drawn in the former hall of patients. Its 8-shaped curve is stretched along a line that crosses the entire width of the room, engraved in the slabs of the floor, and shows the hour of the true as well as the mean solar noon.
The building has indeed a vast nave, 18 meters wide, 90 long and 27 high. Since the mid-seventeenth century it has ceased to be used as a hospital. After they walled up one of the Gothic windows of the great hall, letting only a thin ray of sunshine to pass through, several observations were necessary to level the horizontality of the floor, to draw the meridian, to mark to the right and left of this axis the position of the sunspot at noon. It was Joseph Lalande, astronomer, encyclopedist, director of the Paris Observatory, member of the Academy of Sciences, and future creator of the Bureau des Longitudes, who realized all the calculations and verifications. The ensemble was inaugurated in October 1786.


Around noon, the sunbeam passing through the hole drilled in a former window of the southern wall, forms a light spot on the ground. It is solar noon when the sunspot reaches the southernmost point of its course. At this moment, the light spot falls exactly on the north-south line drawn on the floor. This line is the intersection of the meridian’s plane and the horizontal plane.
The straight line of the true solar noon is surrounded by an extended 8-shaped curve indicating the mean noon. It thus integrates the shift called equation of time: when it is mean noon, the light spot falls on the 8-shaped curve, which approaches or moves away from the wall, following the apparent height of the sun. In winter, the spot crosses the meridian increasingly farther from the entry point – so far indeed, that the hall was not wide enough, and it was necessary to carve a hole in the opposite wall, to finish drawing the curve. In summer, on the contrary, the light spot is closer and closer to the entry point and the foot of the southern wall. These two extremes correspond to the winter and summer solstices. The line joining them exactly shows the north-south direction, drawing on the floor the local meridian – that is, the meridian of Tonnerre.

Thus the meridian of Tonnerre translates in an immediately readable way a wealth of cosmographical information, erudite ones on the one hand, worthy of the era of the Enlightenment, and inherited from ancient traditions on the one hand: the orientation of the meridian (the north-south axis), the inclination of the elliptic curve, the true time, the mean time, the solstices and equinoxes (the four times of the year when the real time and mean time coincide), the months, the seasons and the zodiacs.

However, as this meridian was drawn in a thirteenth-century building, and when I started to look for its history, I was not aware of its true date of creation, I began to research how they calculated the time in the Midle Ages. After all, there is also a beautiful medieval sundial on the external wall of this hospital. And even if it is far from Cassini and from the meridians, it is not without interest – and neither is irrelevant.
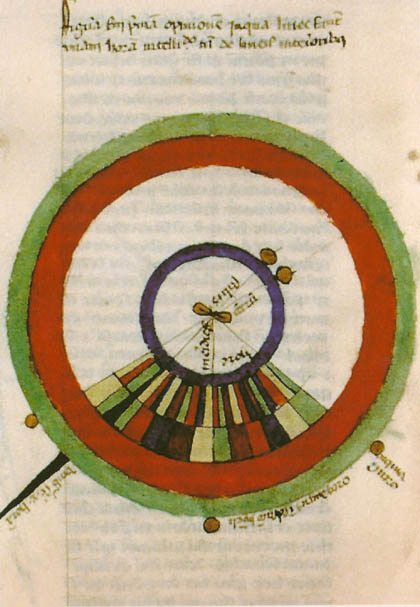
To design a sundial, they had to measure the length of the daylight, divide it in hours, and correct them according to the seasons. The length of the day and of the night, dependent on the seasons and on the latitude, is the subject of the following page of this fifteenth-century Bréviaire d’amour. The three concentric circles reflect the relationship of the division of the hours and the length of the day at the equinox (the central circle) and the solstices (winter in the bottom, and summer in the top).
Sometimes the length of the day and of the night assumes apparently absurd proportions – but these are miraculous moments, when God plays with time, and reverses the course of the sun for a short while. The exegete Nicolas of Lyra, in his Postilla super totam Bibliam written in the middle of the fifteenth century offers a concrete illustration to a passage of Isaiah: the shadow of the sun steps back to “the stairs of Achaz” (Is 38:8), and thus then covers – depending on the dial – ten or twenty additional divisions, resulting in a daylight of 22 or even 32 hours. In the illustration, to the left, on the ruler under the hour circle, we see the shadow of the stylus extending by way of a sundial to the tenth hour.
 Bartholomaeus Anglicus, On the properties of things, Eastern France, ca. 1480, Tours, BM, ms. 703, f. 176v
Bartholomaeus Anglicus, On the properties of things, Eastern France, ca. 1480, Tours, BM, ms. 703, f. 176vTo measure the time by daylight, the observer can use an astrolabe, or elevate to his eyes a so-called “old-style” quadrant, a device which related the height of the sun to the latitude where the observer stood, by way of a quarter of a circle provided with a system of degrees and a plummet, associated with a cursor moving along the degrees, which measured the meridian height of the sun. The following image is disturbing since it combines the observation of the sun at its zenith with a group of stars – but perhaps the instrument could be used either day and night.
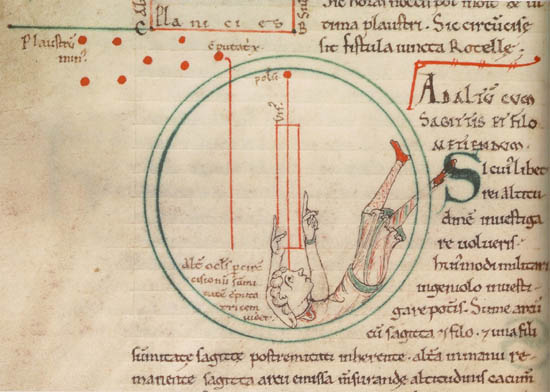
For the hours of the night, they relied on the rotation of the heavens: if they knew the midnight position of a circumpolar star, its various positions allowed to determine the time. The person, lying in such a strange upside down position in the 12th-century manuscript, obviously does not use a telescope, but watches the pole through a tube. Above him, we can identify the Little Bear near the observed star, the computatrix or “calculator”, aligned with the axis of the tube.
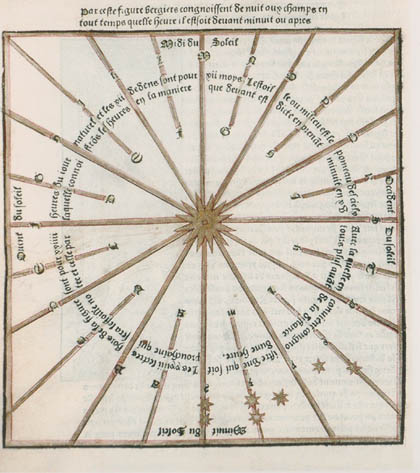
And finally we come to what is beyond my comprehension: to calculate the time at night, by using a simple rope held so that it coincides with the star representing the pole. Parting from this, one imagines a figure centered on this star, and divided into 24 sectors, in which one establishes the position of a star “before” or “after” the rope for the hours before or after midnight. Since sidereal time differs from the solar hour 4 minutes per day (which means a cumulative difference of one hour in 15 days), the 24 lines in the figure serve to adjust the position of the star according to this change (this is the role of the shorter lines). I wonder how many shepherds, walking the dark paths through the night, with a rope in the hand, were able to measure and calcuate the time. Nevertheless, you will find the same figure on the Saxon sundial in Yorkshire below, made around 1060, with its alternating long and short lines.

 Bartholomaeus Anglicus, On the properties of things, Paris, before 1416, Reims, BM, ms. 993, f. 130r
Bartholomaeus Anglicus, On the properties of things, Paris, before 1416, Reims, BM, ms. 993, f. 130rNote that besides the quadrant, the observer of the sky could also use an armillary sphere, whose rings and armlets symbolized the remarkable circles of the celestial sphere, by way of a model of the universe. The scaled armillary spheres could adjust the observations to the latitude, mainly for the pedagogical purposes of the memorization of the reference points in the sky, to visualize and solve simple problems related to the apparent movement of the sun or the stars, or, once again, were used to calculate the hours of the day and the night.
“What, then, is time? If no one ask of me, I know; if I wish to explain to him who asks, I know not … But do I thus measure, O my God, and know not what I measure?”
St. Augustine: Confessions XI.






























































2 comentarios:
For another perspective on the path traced by the sun see this analemma composed at Baku.
A beautiful echo of the drawingon the ground, especially with Venus as a guest star.
Publicar un comentario